Воєнно-ліричний відступ № 3
Микола Жарких
: «Увечері 28 серпня російська авіація увійшла в повітряний простір Білорусі із РФ і випустила по території України не менше п’яти ракет». (29 серпня 2022 р. о 7:45).
Якщо якісь там «білоруси» в лапках і в штатському, або білоруси без лапок і в цивільному, або «западно-русские» в лапках і прямо-таки в білоруському (чи навіть у «западно-русском») думають, що ми щось їм забудемо і подаруємо – то їх надії марні. Вони ще будуть бігати по всьому світу і просити ув’язнити їх у броньованих камерах, рятуючись від нашої помсти. Але броньовані камери їм не допоможуть.
Це я Олегу Ліцкевичу на замітку…
Інтеграл, виписаний вище, дає нам імовірність влучання лапте-ракети в певну область R. Але мене більше цікавить імовірність враження враження конкретної цілі PM (ну, від Mykola Zharkikh).
Для цього нам треба ввести ще одну густину імовірності A (affect):
A = A(rH, rM)
аргументами якої виступають два радіус-вектори: точки влучання лапте-ракети H (hit) і точки розміщення цілі M.
При цьому слід знати, що для лаптеносних лаптів кожна точка, куди падає їх ракета, автоматично становиться ціллю атаки. Наприклад, ракета ціною в 10 мільйонів доларів упала в лісі і струсила всі горіхи з куща ліщини – ну бодай такої шкоди хохлам наробили. Тому в лапте-звітах усі ракети завжди влучають у свої цілі і ні одна не пролітає мимо.
По науці це виглядає так:
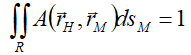
де інтегрування ведеться саме по rM. Простою мовою, якою б не була точка «прицілювання» rH, ракета кудись-то попаде, і тільки треба сказати: «От туди ми, лапті, і хотіли влучити».
Імовірність ураження цілі в точці rM дає формула
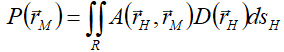
де інтегрування ведеться по rH.
