Початкова сторінка

Микола Жарких (Київ)

Персональний сайт

?
Лист на сайт
Стрічка новин (RSS)

Текстологія

Микола Жарких

Війна на виснаження Гнило-Солом’яної Орди йде повним ходом. 500 убитих пушкіністів на день уже давно стали нормою, а час від часу повідомляють і про 800 з гаком. А от 5 січня 2023 р. повідомили ще й про 12 знищених артилерійських систем. Чи не наслідок застосування нової системи контрбатарейної боротьби, про яку злегка натякали у пресі?

Для нас цілком недостатньо відкинути ворожу армію за наші кордони. Для нашої безпеки потрібна демілітаризована зона на території Орди. А оскільки дальність польоту їх крилатих ракет досягає 5500 км, то ця зона мусить простягаться на схід принаймні до Якутська (5300 км від Біловодська в Луганській області, а це – теж Україна; 7 січня 2023 р. о 8:40).

Попередній огляд і картографування безспірних назв показав дві дуже суперечні між собою тези:

1, безсумнівно, переліки назв у різних ярликах якось пов’язані між собою;

2, жоден ярлик не повторює перелік з попередніх ярликів, а завжди дає свій варіант.

Тільки три із 82 назв – Київ, Хотмишль та Яголдаєва тьма – присутні у всіх ярликах, решта назв з’являється, зникає і знову з’являється. Можна спробувати застосувати до текстів переліків кластерний аналіз. Я вже пояснював його методику [Жарких М. І. Дві традиції літописання Великого князівства Литовського. – К.: 2016 р., розділ «Аналіз варіантів тексту Повісті про Свитригайла»], тут не повторюю.

Віддалі між текстами будемо рахувати паралельно за двома методиками. Різницю їх показую на прикладі. Нехай в одному переліку стоїть: Київ – Канів – Черкаси, а в другому – Київ – Черкаси – Канів. Жорсткий метод враховує співпадіння назв і їх позицій, тому в нашому прикладі буде два співпадіння. М’який метод ігнорує позиції – аби тільки назви співпадали, і так буде три співпадіння. Ясно, що м’який метод буде давати число співпадінь більше або рівне тому, що дає жорсткий метод.

В наведеній нижче таблиці вище діагоналі стоять стоять співпадіння за м’яким методом, а нижче діагоналі – за жорстким. З неї бачимо, що пара ярликів 1520 – 1532 рр. має по 40 співпадінь обома методами, а пара 1541 – 1542 рр. – 15 м’яких співпадінь і тільки 8 жорстких.

1461 1472 1507 1513 1514 1517 1520 1532 1539 1541 1542 1552 1560
1461 28 31 25 25 23 23 23 11 25 14 12 11
1472 23 29 31 32 31 29 31 10 29 11 11 10
1507 22 28 45 45 42 37 46 14 41 15 17 16
1513 16 30 45 47 43 42 46 13 40 15 17 16
1514 16 32 45 47 46 41 50 14 43 11 16 15
1517 14 31 42 43 46 39 46 14 45 15 16 16
1520 13 27 37 42 41 39 40 11 36 11 12 13
1532 14 30 44 46 49 45 40 14 42 12 16 14
1539 3 6 10 11 11 11 10 11 14 9 14 14
1541 13 28 31 38 41 42 34 39 13 15 17 15
1542 5 5 7 8 8 7 5 6 6 8 9 8
1552 4 7 12 14 13 13 10 12 14 15 8 21
1560 3 5 9 11 10 10 8 9 11 10 6 19

Тепер число співпадінь (C – coincidence) ми перераховуємо у віддалі між текстами (D – distance) за формулою:

D = 50 / C

Повторюся, що для перерахунку підходить будь-яка спадна функція, так, щоб менше число співпадінь давало більшу відстань.

А число 50? Це – нормувальний множник, поняття, незрозуміле нікому з гуманітаріїв, але добре відоме нам, фізикам-теоретикам (навіть відставним). При такому нормування мінімальна віддаль буде 1 (1514 – 1532 рр. при м’якому рахунку).

Отже віддалі між текстами маємо такі:

1461 1472 1507 1513 1514 1517 1520 1532 1539 1541 1542 1552 1560
1461 1.79 1.61 2.00 2.00 2.17 2.17 2.17 4.55 2.00 3.57 4.17 4.55
1472 2.17 1.72 1.61 1.56 1.61 1.72 1.61 5.00 1.72 4.55 4.55 5.00
1507 2.27 1.79 1.11 1.11 1.19 1.35 1.09 3.57 1.22 3.33 2.94 3.13
1513 3.13 1.67 1.11 1.06 1.16 1.19 1.09 3.85 1.25 3.33 2.94 3.13
1514 3.13 1.56 1.11 1.06 1.09 1.22 1.00 3.57 1.16 4.55 3.13 3.33
1517 3.57 1.61 1.19 1.16 1.09 1.28 1.09 3.57 1.11 3.33 3.13 3.13
1520 3.85 1.85 1.35 1.19 1.22 1.28 1.25 4.55 1.39 4.55 4.17 3.85
1532 3.57 1.67 1.14 1.09 1.02 1.11 1.25 3.57 1.19 4.17 3.13 3.57
1539 16.67 8.33 5.00 4.55 4.55 4.55 5.00 4.55 3.57 5.56 3.57 3.57
1541 3.85 1.79 1.61 1.32 1.22 1.19 1.47 1.28 3.85 3.33 2.94 3.33
1542 10.00 10.00 7.14 6.25 6.25 7.14 10.00 8.33 8.33 6.25 5.56 6.25
1552 12.5 7.14 4.17 3.57 3.85 3.85 5.00 4.17 3.57 3.33 6.25 2.38
1560 16.67 10.00 5.56 4.55 5.00 5.00 6.25 5.56 4.55 5.00 8.33 2.63

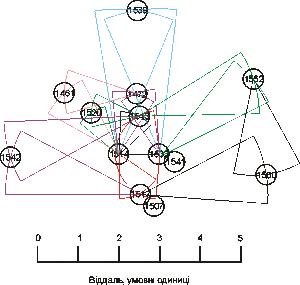
Розглянемо спочатку діаграму на м’яких віддалях. Хід її побудови такий:

База: 1.00 (1514 – 1532);

1513: 1.06 (1513 – 1514) + 1.09 (1513 – 1532);

1517: 1.09 (1517 – 1532) + 1.09 (1514 – 1517);

1507: 1.09 (1507 – 1532) + 1.11 (1507 – 1514); в масштабі креслення позиція 1507 практично співпадає з позицією 1517, тому умовно пересуваємо 1507 вниз і праворуч;

1541: 1.11 (1517 – 1541) + 1.16 (1514 – 1541); в масштабі креслення позиція 1541 практично співпадає з позицією 1532, тому умовно пересуваємо 1541 вниз і праворуч;

1520: 1.19 (1513 – 1520) + 1.22 (1514 – 1520)

1472: 1.56 (1472 – 1514) + 1.61 (1472 – 1532)

1461: 1.61 (1461 – 1507) + 2.00 (1461 – 1514)

1552: 2.94 (1513 – 1552) + 2.94 (1541 – 1552)

1542: 3.33 (1513 – 1542) + 3.33 (1517 – 1542)

1539: 3.57 (1514 – 1539) + 3.57 (1532 – 1539)

1560: 2.38 (1552 – 1560) + 3.13 (1517 – 1560)

Кластерний аналіз на основі м’якої міри

Кластерний аналіз на основі м’якої міри

Як бачимо, збіжність результатів дуже далека від ідеальної. Так, на кресленні положення 1507 і 1517 практично співпадають, а між ними має бути віддаль 1.19; така сама віддаль мала би бути і між 1532 та 1541. Віддаль між 1472 і 1513 на креслені становить 0.56, тоді як фактично (в таблиці) – 1.61, і так далі (той, хто простежив хід побудови, зауважив, що ці три віддалі не використовувались для побудови діаграми, і тому вони можуть служити для її перевірки).

Разом з тим віддаль 1542 – 1560 на діаграмі становить 6.3, а в таблиці маємо 6.25. Віддаль 1542 – 1552 на діаграмі – так само 6.3, в таблиці – 5.56. Віддаль 1539 – 1542 на діаграмі – 4.8, в таблиці – 5.56. Виходить, великі віддалі між текстами прогнозуються краще, ніж малі.

В цілому діаграму можна поділити на три концентри: відносно щільне ядро (1513, 1517, 1532, 1541), проміжну зону (1472, 1507, 1517, 1520) та зовнішню зону (1461, 1539, 1542, 1552, 1560).

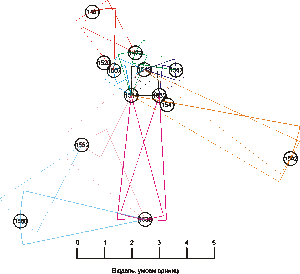
А тепер подивимось, що нам покажуть жорсткі віддалі.

База: 1.02 (1532 – 1514)

1513: 1.06 (1514 – 1513) + 1.09 (1532 – 1513)

1517: 1.11 (1532 – 1517) + 1.16 (1517 – 1513)

1507: 1.11 (1513 – 1507) + 1.11 (1514 – 1507)

1520: 1.19 (1520 – 1513) + 1.22 (1520 – 1514); в масштабі креслення позиція 1520 практично співпадає з позицією 1507, тому умовно пересуваємо 1520 вгору і ліворуч;

1541: 1.19 (1541 – 1517) + 1.22 (1541 – 1514); в масштабі креслення позиція 1541 практично співпадає з позицією 1532, тому умовно пересуваємо 1541 вниз і праворуч;

1472: 1.56 (1514 – 1472) + 1.61 (1517 – 1472);

1461: 2.17 (1472 – 1461) + 2.27 (1507 – 1461);

1539: 4.55 (1539 – 1514) + 4.55 (1539 – 1532);

1542: 6.25 (1542 – 1513) + 6.25 (1542 – 1514);

1552: 3.57 (1552 – 1513) + 3.57 (1552 – 1539);

1560: 2.63 (1560 – 1552) + 4.55 (1560 – 1539);

Кластерний аналіз на основі жорсткої…

Кластерний аналіз на основі жорсткої міри

Проблеми із неузгодженостями малих віддалей, відзначені вище, спостерігаються і тут. Із великими віддалями справа стоїть краще: 1542 – 1560 на діаграмі 10.1, в таблиці – 16.67; 1542 – 1552 на діаграмі 7.6, в таблиці 6.25; 1461 – 1542 на діаграмі 8.94, в таблиці 10.

В цілому поділ текстів на три концентри зберігається і при застосуванні жорсткої міри, хіба що зовнішня зона виглядає виразніше, її відстані від ядра значно більші.

Отже, жорстка міра, котра до певного ступеня враховує структурну подібність / неподібність текстів, здається більш пожиточною.

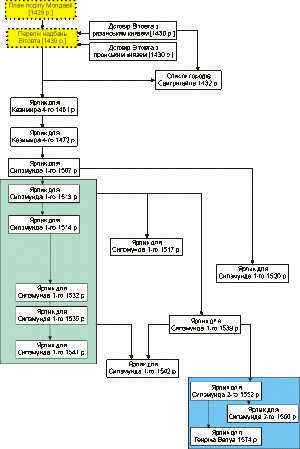
Залежність текстів можна виразити наступною стеммою:

Стемма текстів ярликів

Стемма текстів ярликів

При її побудові враховано: 1, хронологію документів; 2, спостереження над переліком безспірних об’єктів, винесені на подані вище картосхеми; 3, результати кластерного аналізу.