12. "Smolensk" group (No. 286 – 298)
Nicholas Zharkikh
Shortened text of the section. Full text in ukrainian version.
: tonight, the russian Shaheds were circling Ukraine and trying to hit Kyiv from the north-eastern direction. All of them were destroyed on the approaches to the capital, there were no casualties or damage. I personally didn’t hear anything because my windows face southwest, sounds from the northeast don’t reach me well (Jun 20, 2024 at 7:50 am).
The "Smolensk" group of objects in the SRG begins with the appropriate title "A se smolenskyi" (= there are Smolensk’s) and Smolensk is in the first place in it. This is a unique phenomenon among SRG headlines.
(286) Smolnesk on the Dnieper (287)
Undisputed modern city (Russia), which really stands on the Dnieper (and the SRG was not mistaken in this detail!). Probability class – A.
(288) Elno
Modern town 75 km east of Smolensk (Russia). Probability class – A.
(289) on Ima [river]
Unknown object. Probability class – D.
(290) Vyazma
Modern town in the Smolensk region (Russia). Probability class – A.
(291) Dorogobuzh
Modern town on the Dnieper 82 km east of Smolensk (Russia). Probability class – A.
(292) Mstislavech
It is assumed that it is a near Dorogobuzh. Probability class – C.
(293) Mstislav
A modern town in the Mogilev region of Belarus. Probability class – A.
(294) on Vekhra [river]
Mstislavl really stands on the river, which is now called . It flows into the Sozh 9 km east of Mstislavl. Probability class – A.
(295) Obolensk
Doubling Obolensk’s record (No. 242). Probability class – G.
(296) Kozelesk
Duplication of Kozelsk record (No. 251) Probability class – G.
(297) Vyatchesk
There are no about this object. Probability class – D.
(298) Rzhavesk
Unknown name. Probability class – D.
Thus, out of 13 objects of the "Smolensk" group, we have 7 undisputed (54 %), one is attributed to trouble, three are unknown and two are duplications. The quality of SRG in this part is low, not better than the previous group.
Maps
The small "Smolensk" group is of poor quality, but compact. The optimal route is obvious: 293 → 286 → 288 → 291 → 290 = 274 km. It is plotted on the following diagram with blue arrows.
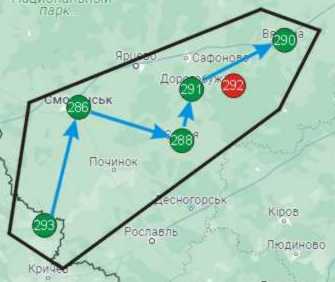
"Smolensk" group. Optimal route
To lay the main real route (between objects of class A), you just need to look at the list: 286 → 288 → 290 → 291 → 293 = 394 km. It is plotted in the following diagram with red arrows. Entropy-A = 144 %.
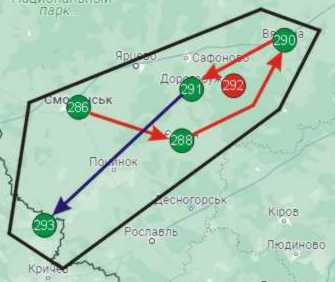
"Smolensk" group. Real route (class A)
Complete real route (classes A + B): 286 → 288 → 290 → 291 → 292 → 293 = 297 km, which gives us entropy-B = 145 %. Arrows of different colors do not have a special meaning, only so that there is no confusion when crossing. There is only one conditionally localized object in the group, so the increase in entropy is negligible.
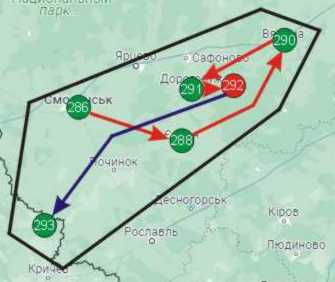
"Smolensk" group. Real route (classes A + B)
The polygon that covers all objects of the group is marked with a black contour on the map. Its diameter (290 – 293) is 212 km. There are no foreign objects in the group.
