Colloid science
Absorption oscillations and low-frequency dispersion
In 1978, after the graduating from University of Kiev, I started working as a physicist-theoretisian at the A.V.Dumanski Institute of Colloid Chemistry and Water Chemistry of Academy of Sciences of the Ukraine (now the National Academy of Sciences of Ukraine). The was the theoretical division in the institute, headed by Doctor of Chemistry Stanislav Samoilovych Dukhin. In the same department worked candidate (now – Doctor of Sciences) Vladimir Nikolajevich Shilov. They were my teachers and I am very grateful to them for help in my professional growth.
Work in the department was carried out in the collective style. The new literature on the problem, each step of calculations, the conclusions from them, and directions for further research – all those were the subject of daily conversations with interested colleagues and managers. Often, nearly a monthly, the department seminars were conducted to discuss complete articles of staff and new problems. We also had presented our works at the Institute conferences and the Seminar on electrosurface phenomena that a some times a year held at the Institute. This style of scientific life promoted professional our growth, was a counterweight to overly narrow specialization, and oblige each collaborator to understand the whole article, not only fragments, which he carried out personally. So, when I shall take the expressions such as "I researched, "I wrote" – one should understood that this reduced form of "I together with his co-authors participated in the research / writing".
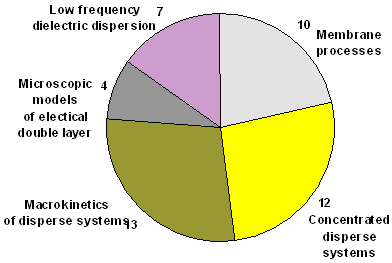
Distribution of papers on topics
Please be aware that the term "colloid science" to denote the discipline, which deal with colloidal state, did not exist at that time – it has acquired rights of citizenship during my work. At that time term "colloidal chemistry" was used, that certainly narrowed the subject, since such phenomena as Tyndall effect (scattering of light beam when passing through colloidal system) have no direct relationd to chemistry.
Piezodialysis
The first focus of my work was piezodialysis – exotic membrane desalination process. This phenomenon has been observed on membranes of the special structure – the charge-mosaic, which consisted of fragments cationite and anionite ion exchange polymers. When bursting of water under pressure through this membrane, it showed higher permeability for dissolved salts than for water, filtrate was more concentrated, and the solution over the membrane was desalinated. I wrote a review of literature on this subject, and later, when cell modes was developed, applied it to macroscopic theory of piezodialysis.
Cell model
Another topic was the study of concentrated disperse systems. By the time all the theoretical studies of the colloidal solution had forced limited idealized model: one particle in the infinite volume solution. The interaction between the particles naturally neglected. This corresponded to a very limited number of systems – in most experiments the concentration of particles was such that their interaction play a role.
For incorporation of the interaction of particles we have developed Cell model. The approach was borrowed from the hydrodynamics of concentrated suspensions and generalized to account for the complex electrical and diffusion phenomena. This synthesis was done using the methods of thermodynamics of irreversible processes. The expression for local entropy production was formulated, which included a contribution of fluid flow, and contributions from current and diffusion fluxes of dissolved substances. All these contributions was cross linked due to the electric charge of colloidal particles (more precisely, the electric double layer, consisting of charges on the particle surface and compensating diffusion layer in solution).
From the expression for entropy production the matrix of kinetic coefficients was derived, which described both direct and cross-transport processes. Direct processes – a movement due to gradient of affine thermodynamic potential, such as the movement of electric charges (ions) under the influence of electric potential difference. Cross-process – a movement under the gradient of another (not affine) thermodynamic potential, for example, elektroosmosis is fluid flow under the influence of the voltage.
Matrix of kinetic coefficients give simple and clear classification for all variety of cross-effects. For example, sedimentation potential (potential difference, which occurred in the process of settling clouds of colloidal particles) can be calculated knowing the speed of electrophoresis (movement of colloidal particles in an electric field) and electrical conductivity of suspension.
Our cell model provided that the total entropy production in the system is the sum of the contributions of individual cells and cell contribution was an integral of local fields by cell volume. In this way, all the kinetic coefficients acquired dependence on volume fraction of particles – the most important parameter of concentrated disperse systems.
This original method of calculation laid the basis for two theses – my and Y.B.Borkowski, and entered the practice of research, even in textbooks.
Streaming variables
Another interesting and useful trick, formulated in the process of cell model elaboration, was the splitting of electrical and diffusion fields on stream and semi-equilibrium parts. Analyzing the expression for entropy production, I had notified that not all the electric field generate current (and thus entropy): within electric double layer potential drop (and electric field) exist, but at steady state there is no electrical current. Nonequilibrium conditions created by external influences should be considered as a small deviation from equilibrium, and semi-equilibrium field, although different from the true equilibrium, can not causing the production of entropy. So, for calculation of the kinetic coefficients the detailed calculation semi-equilibrium fields in general was not necessary – it was necessary count only streaming fields.
This method dramatically simplify all mathematical derivations and could be applied universally to any problems – for one particle, and for concentrated suspensions as well. Later, this method is the most general form was systematically developed by V.N.Shilov in his doctoral dissertation.
Using these methods developed by us, a series of articles was prepared, where dependence of some particular kinetic coefficients on volume fraction were explored. The most interesting was this dependence for the conductivity. It was found that particles with small surface conductivity, which at low volume fractions reduced conductivity with increasing of volume fraction could lead to an increase in the conductivity of solution. It is possible to explain the results of some experiments where such unusual dependence of the conductivity of the volume fraction was observed. Thus our cell model won first experimental confirmation.
Another surprising result of calculations for cell model – the circumstances was found under which the filtering of electrolyte through a porous wall caused outgoing solution to become more concentratred. Fundamentally it was the same as piezodialysis, only within homogeneously charged diaphragm. The rate of effect was small but could have some importance, for example, during the filtration of saturated salt solution through rocks: even a small concentration could exceed the threshold of solubility and cause deposition of crystals.
Reverse osmosis
For other parameter sets our calculations showed that the outgoing electrolyte solution, by contrast, desalinated. It was the phenomenon of reverse osmosis, which at that time was already widely used for the desalination of sea and brackish water for obtaining of drinking and industrial water. But its nature, the factors that determine the suitability of membranes for reverse osmosis, were unknown. Electric double layer on the surface of the membrane matrix, which we have studied in our models, gave a reverse osmosis effect, but it quickly declined with increasing concentration and for sea water fall almost to zero. In all years of my work in colloid science reverse osmosis mechanism remained a mystery.
Disjoining pressure
Another area of application of the cell model was disjoining pressure investigation. According to the Deryahin-Landau theory (reliably confirmed experimentally), the main factor of stability of colloidal systems was disjoining pressure of the electric double layers. This pressure prevent coalescence (coagulation) of particles and loss of sediment from the colloidal solution. Traditionally, the model used for calculations of disjoining pressure was flat capillary between two particles. After our own calculations the volume fraction of particles was introduced in the theory of stability as a parameter. Wirhin this model, a theory of electrostatic swelling pressure was developed.
These works formed the basis of the theory of dynamic membranes. Normal static membrane created from crosslinked polymer film; dynamic membrane formed on its surface during filtering of colloidal solution. Colloidal particles, having no chance to penetrate the small pores in the skeleton, stayed on its surface, forming a kind of jelly – the layer with a high concentration of colloidal particles. This layer under certain conditions does not coagulate and retained its fluidity. In our model this layer was pressed with fluid flow through the membrane and stabilized with disjoining pressure of double layers; this led to changes in volume fraction of particles across the membrane. Transport processes in this layer was modelled as well.
My interest in membrane processes is also evident in another direction. After reviewing the experimental data by T.V. Knyazkova on selectivity of reverse osmosis membranes, we (I and Andrew Yaroshchuk) found ingenious coordinates in which the dependence of selectivity on membrane permeability assuming a simple form. For this we had to learn good techniques of mathematical statistics to scrapping of erroneous observations (related to the defective membrane) and then to achieving the normalization of the distribution remains. The article, which was published by us, provided as a theoretical basis for scrapping defective membranes.
Incomplete equilibrium
Another area of membrane research was related to the transference numbers – the kinetic coefficients, which determine the contribution of certain ions for conductivity of membranes. This phenomenon was not my goal by itself (there was difficult to say anything new about it), but in connection with the new direction of my research – the theory of incomplete equilibrium. Incomplete equilibrium occurs when at least one of the eigenvalues of the kinetic coefficients matrix became zero (degenerate matrix). Interesting universal correlation between the thermodynamic potentials was appeared in this situation, which were visible manifestations of incomplete equilibrium. Unfortunately, I was unable to systematically develop and publish these studies.
Structural independence
One article (with Andrew Yaroshchuk) was devoted to the new case of the structural independence of electrokinetic phenomena. The first result in this direction was obtained by M. Smoluchowsky in 1905. He proved that electroosmosis speed (movement of fluid under the influence of an electric field) does not depend on the structure (form of capillary networks) of the disperse systems, if the electric double layer is thin compared with the diameter of capillaries. The result was so elegant that impressed all who first encountered him. And so we were establich similar structural independence in the opposite case – when the thickness of electric double layer is larger than the diameter of the capillaries.
Ionophoresis
The next group of my articles was devoted to the study ionophoresis. In colloidal systems (and in solutions in general), there is no electric current as is – the ions always act as charge carriers. Therefore, electric current and diffusion flows can be arranged as a combination of individual ions flow. The expression for entropy production has been transformed into a sum of contributions from individual ions flow caused by variations of respective electrochemical potentials. The brillaint symmetry of thermodynamic forces and flows was established that dramatically simplified consideration of multicomponent solutions (those that contain ions in more than two species; all previous theoretical models were limited to case of one type of cations and one of anions). In its pure form ionophoresis of colloids (ie, movement of colloidal particles in the field of electrochemical potential gradient only for one sort of ions) could hardly observed somewhere in the experiment, but as a theoretical approach to consider the entire series of kinetic phenomena, it has no competitors.
In the last years the Soviet Union existence we had established a lively scientific contacts with the Computing Center in Scientific Center of Biological Research (Puschino over Oka river near Moscow). Our colleagues from the Center had a very different training – they were mathematicians, for whom the qualitative theory of differential equations was the simplest thing (while I have no experience in this field). They were involved in modeling of transport processes in biological structures, and our results on ionophoresis were extremely interesting for them, because for biological systems the presence of several types of ions is a rule, not the exception. As the result of collaboration were the articles on ionophoresis and diffusiophoresis published by I and Gennady Denisov.
Modeling heterogeneity
Each colloid system is an example of heterogeneity, it is heterogeneous because it contain the dispersed phase. But in such systems there are other levels of heterogeneity – both larger and smaller than colloidal particle. Heterogeneity with the scale smaller than colloidal particle size associated with the discreteness of charges. Electric charge of particles formed by ionization centers on its surface. If the concentration of these centers is high, they placed closely and their discreteness can be neglected, considering the charge distributed evenly across the surface. This assumption was common for all the theoretical models. If this concentration is low, surface can be treated as a mosaic, formed from the elementary charge and uncharged areas. Attempts to mathematical modeling of this phenomenon led me to the concept of mosaic surface layer. Mosaic have the effect when the thickness of this layer exceeds the thickness of the double layer.
Heterogeneity with the scale larger than particle size was modeled by me as variations in volume fraction of particles. I examined the impact of this phenomenon in the electrical conductivity of system.
Another aspect of this heterogeneity was associated with electrodes, which always present in measurement. In an alternating electric field, which is commonly used during the conductivity measurements, colloidal particles serving electrophoretic oscillations. Those oscillations for particles that are near the electrodes, leads to the oscillations of polarization charges quotes that are allocated on the electrode, which is shown as an additional current. I researched this bizarre mechanism, which shows that even for such a simple thing as passing an electric current, the global inhomogeneity of the system in the form of electrodes is of some importance.
Absorption oscillations and low-frequency dispersion
Very interesting new aspect has been studied by me in phenomenon of low frequency dielectric dispersion of colloidal solutions. This phenomenon was established experimentally for a long time. It was the fact that the water dispersion of colloidal particles under low frequency electric field showed very high capacity (permittivity), like ferroelectrics. The basic theoretical model of this bright effect was built by Dukhin and Shilov. The reason of such unusual capacity was the concentration polarization of thin double layer of particles.
This theory is well consistent with the experiment and was generally recognized as a cause of the phenomenon. But a more detailed review showed that the theory provided a maximum permittivity, which does not depend on any system parameters. Experimentally observed values of permittivity was higher than this threshold, and it was no idea what additional processes contribute to this phenomenon.
The theoretical consideration was limited to a binary electrolyte model (one specia of cations and anions). Introduction of more species of ions only complicated calculations and had seems not brought anything new in the picture as whole. Changes of concentration of ions, which were primary cause of dispersion, were limited by the condition of local electroneutrality of double layer.
I noticed that in the case of two species of counterions the condition of local electroneutrality not so much limits the concentration drops, because increasing the concentration of one counterion could compensated by decreasing the concentrations of another counterion. This idea proved to be very promising and led the set of papers. The main mass of calculations was carried out by me and Elijah Razilov. Our calculations show that these adsorption oscillations may indeed increase the permittivity of system above the threshold for binary systems.
Thus were the main results of my research in colloid science.

