Коллоидная наука
Колебания адсорбции и низкочастотная дисперсия
В 1978 году после окончания Киевского университета я начал работать как физик-теоретик в Институте коллоидной химии и химии воды им.А.В.Думанского Академии наук УССР (ныне Национальной Академии наук Украины). В институте был теоретический отдел, которым руководил доктор химических наук Станислав Самойлович Духин. В этом же отделе работал кандидат (ныне – доктор физико-математических наук) Владимир Николаевич Шилов. Они были моими учителями, и я искренне благодарен им за помощь в моем профессиональном росте.
Работа в отделе была коллективной в наилучшем и полном смысле. Новая литература, постановка задач, каждый шаг вычислений, выводы из них и направления дальнейших исследований – все это было предметом ежедневных заинтересованных бесед с коллегами и руководителями. Часто, почти каждый месяц, проходили семинары отдела, на которых обсуждались законченные статьи сотрудников и новые проблемы. Выступали мы также на конференциях Института и на всесоюзном семинаре по электроповерхностным явлениям, который по несколько раз в год проводился на базе Института. Такой стиль научной жизни способствовал профессиональному росту, был противовесом чрезмерно узкой специализации и обязывал каждого соавтора разбираться в всей статье, а не только в том фрагменте, который выполнял лично он. Поэтому, когда я ниже буду употреблять выражения «я исследовал», «я написал» – следует понимать, что это сокращенные формулы «я совместно со своими соавторами принимал участие в исследовании / написании».
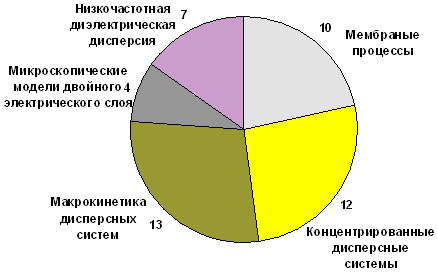
Распределение работ по темам
Следует знать, что термина «коллоидная наука» для обозначения дисциплины, имеющей предметом коллоидное состояние вещества, тогда не существовало – он приобрел прав гражданства уже за время моей работы. В то время употреблялся термин «коллоидная химия», что бесспорно, сужало предмет, поскольку такие явления, как эффект Тиндаля (рассеивание света в сторону при прохождении луча через коллоидную систему) непосредственного отношения к химии не имеют. Из-за этой особенность и моя диссертация, посвященная применению методов теоретической физики для моделирования поведения коллоидных систем, принесла мне степень кандидата химических наук. Степени по физико-математическим наукам за коллоидные исследования начали присуждаться позже.
Пьезодиализ
Первым направлением моей работы был пьезодиализ – экзотический мембранный процесс опреснения воды. Это явление наблюдалось на мембранах специальной структуры – зарядово-мозаичных, которые состояли из фрагментов катионитного и анионитного ионообменных полимеров. При продавливании воды через такую мембрану она проявляла большую проницаемость для растворенных солей, чем для воды, фильтрат оказывался более концентрированным, а раствор над мембраной опреснялся. Я написал обзоры литературы по этому предмету, а позже, когда была построена ячеечная модель, применил ее для макроскопической теории пьезодиализа.
Ячеечная модель
Следующей темой было исследование концентрированных дисперсных систем. До того времени все теоретические исследования коллоидных растворов были вынужденно ограничены идеализированной моделью: одна частица в бесконечном объеме раствора. При этом взаимодействие частиц между собой, естественно, игнорировалось. Это соответствовало довольно ограниченному кругу систем – в экспериментах чаще концентрация частиц была такой, что их взаимодействие играло роль.
Для учета взаимодействия частиц нами была разработана ячеечная модель. Подход был заимствован из гидродинамики концентрированных суспензий и обобщен для учета комплекса электрических и диффузионных явлений. Это обобщение было сделано с применением методов термодинамики необратимых процессов. Было сформулировано выражение для локального производства энтропии, которое включало как вклад от потока жидкости, так и вклады от электрического тока и диффузионных потоков растворенных веществ. Все эти вклады причудливо переплетались благодаря наличию у коллоидных частиц электрического заряда (точнее, двойного электрического слоя, который состоял из зарядов на поверхности частицы и компенсирующего диффузного слоя в растворе).
Из выражения для производства энтропии следовала матрица кинетических коэффициентов системы, которая описывала как прямые, так и перекрестные процессы переноса. Прямые процессы – это движение под действием перепада сродного термодинамического потенциала; например, явление электропроводности является движением зарядов (ионов) под действием перепада электрического потенциала. Перекрестные процессы – это движение под действием перепада другого (не сродного) термодинамического потенциала; например, электроосмос является движением жидкости под действием электрического напряжения.
Матрица кинетических коэффициентов давала простую и понятную классификацию всего многообразия перекрестных явлений. Например, потенциал седиментации (разность потенциалов, которая возникала в процессе оседания облака коллоидных частиц) можно было вычислить, зная скорость электрофореза (движения коллоидных частиц в электрическом поле) и электропроводность суспензии.
Примененная нами ячеечная модель предусматривала, что суммарное производство энтропии в системе равна сумме вкладов отдельных ячеек, а вклад ячейки вычислялся как интеграл локальных полей по ее объему. Таким образом все кинетические коэффициенты приобретали зависимость от объемной доли частиц – важнейшего параметра концентрированной дисперсной системы.
Этот оригинальный метод расчета лег в основу двух диссертаций – моей и Ю. Б. Борковский, и вошел в практику исследований, даже в учебники.
Потоковые переменные
Еще одним интересным и полезным приемом, сформулированным в процессе работы над ячеечной моделью, было разделение электрических и диффузионных полей на квазиравновесные и потоковые части. Анализируя выражение для производства энтропии, можно было заметить, что не каждое электрическое поле порождает ток (и, соответственно, энтропию): в двойном электрическом слое перепад потенциала (и электрическое поле) есть, но в равновесном состоянии никакого электрического тока нет. Неравновесные условия, созданные внешними воздействиями, следует рассматривать как небольшое отклонение от равновесия, и квазиравновесные поля, хотя и отличались от истинно равновесных, все же не вызывали производство энтропии. Следовательно, для вычисления кинетических коэффициентов детальный расчет квазиравновесных полей вообще оказался не нужным – надо было рассчитывать только потоковые поля.
Этот прием кардинально упрощал все математические выкладки и мог универсально применяться в отношении любых задач – как для одной частицы, так и для концентрированной суспензии. Позднее этот метод в самом общем виде был систематически развит В. М. Шиловым в его докторской диссертации.
С использованием развитых нами методов была написана серия статей, посвященных зависимости отдельных кинетических коэффициентов системы от объемной доли частиц. Наиболее интересной оказалась эта зависимость для электропроводности. Было обнаружено, что частицы с небольшой поверхностной проводимостью, которые при малых объемных долях уменьшали электропроводность, с ростом объемной доли могли приводить к увеличению проводимости раствора. Это позволило объяснить результаты некоторых экспериментов, где наблюдалась эта необычная зависимость электропроводности от объемной доли. Так наша ячеечная модель получила первое экспериментальное подтверждение.
Еще одним неожиданным результатом расчетов по ячеечной модели было выявление режима, когда при фильтрации электролита через пористую перегородку происходило концентрирования вытекающего раствора. Принципиально это был тот же пьезодиализ, только на однородно заряженных диафрагмах. Количественно эффект был небольшим, но мог иметь определенное значение, например, во время фильтрации насыщенного раствора слаборастворимых солей через горные породы: даже незначительное концентрирования могло превысить порог растворимости и вызвать отложения кристаллов.
Обратный осмос
Для других режимов наши расчеты показывали, что при фильтрации электролита исходящий раствор, наоборот, обессоливается. Это было явление обратного осмоса, которое к тому времени уже достаточно широко использовалось для опреснения морских и солоноватых вод и получения питьевой и технической воды. Но природа его, факторы, которые определяли пригодность мембран для обратного осмоса, были неизвестны. Двойной электрический слой на поверхности матрицы мембраны, который мы изучали в своих моделях, давал определенный эффект обратного осмоса, но он очень быстро снижался с ростом концентрации раствора и для морской воды падал практически до нуля. За все годы моей работы в коллоидной науке механизм обратного осмоса оставался загадкой.
Расклинивающее давление
Еще одним направлением применения ячеечной модели было изучение расклинивающего давления. Согласно теории Дерягин-Ландау (надежно подтвержденной экспериментально), основным фактором стабильности коллоидных систем было расклинивающее давление двойных электрических слоев. Это давление предотвращало слипание (коагуляцию) частиц и выпадению твердого осадка из коллоидного раствора. Традиционно для модельных расчетов этого давления рассматривался плоский капилляр между двумя частицами. Нашими же расчетам в теорию устойчивости была введена объемная доля частиц. На этой модели построена теория электростатического давления набухания: концентрированная суспензия заряженных частиц, сжатая выше определенной объемной доли, пытается вернуть себе воду, которой не хватает для равновесия (это и есть набухание). Если она при этом замкнутая в некой оболочке, она оказывает давление на оболочку (давление набухания), который я рассчитывал с помощью ячеечной модели.
Эти работы легли в основу теории динамических мембран. Обычная статическая мембрана формировалась из прочно сшитого полимерного каркаса; динамическая мембрана создавалась на поверхности статической во время фильтрации коллоидного раствора. Коллоидные частицы, не имея возможности проникнуть в мелкие поры каркаса, задерживались на его поверхности, образуя своеобразный кисель – слой с высокой концентрацией коллоидных частиц. Этот слой при определенных условиях не коагулировал и сохранял свою текучесть. В нашей модели этот слой сжимался потоком жидкости сквозь мембрану и стабилизировался расклинивающим давлением двойных слоев; это приводило к изменению объемной доли частиц по сечению слоя. Моделировались также процессы переноса в таком слое.
Мой интерес к мембранных процессов проявился также в другом направлении. Проанализировав экспериментальные данные Т. В. Князьковой по селективности мембран для обратного осмоса, мы (я и Андрей Ярощук) обнаружили хитроумные координаты, в которых зависимость селективности от проницаемости мембран приобретала простой вид. Для этого нам пришлось хорошо освоить методы математической статистики, провести отбраковку ложных наблюдений (связанных с дефектами мембран) и потом долго добиваться нормализации распределения остатков. Статья, которая была нами напечатана, предоставляла теоретический базис для отбраковки дефектных мембран.
Неполная равновесие
Еще одно направление мембранных исследований было связано с числами переноса – кинетическим коэффициентами, которые определяют вклад ионов определенного сорта в электропроводность мембран. Числа переноса интересовали меня не сами по себе (здесь трудно было сказать что-то новое), а в связи с новым направлением моих исследований – теорией неполного равновесия. Неполное равновесие имеет место, если хотя бы одно из собственных чисел матрицы кинетических коэффициентов системы обращается в ноль (матрица вырождается). При этом возникали интересные универсальные зависимости между термодинамическими потенциалами, которые были видимыми проявлениями неполного равновесия. К сожалению, эти исследования мне не удалось систематически развить и опубликовать.
Структурная независимость
Одна статья (вместе с Андреем Ярощука) был посвящен новому случае структурной независимости электрокинетических явлений. Первый результат в этом направлении получил М. Смолуховский в 1905 г. Он доказал, что скорость электроосмоса (движения жидкости под действием электрического поля) не зависит от структуры (формы капиллярной сетки) дисперсной системы, если двойной электрический слой является тонким по сравнению с диаметром капилляров. Результат был столь элегантным, что поражал всех, кто впервые с ним сталкивался. И вот нам удалось показать аналогичную структурную независимость в противном случае – когда толщина двойного электрического слоя оказывается больше диаметр капилляров.
Ионофорез
Следующая группа моих статей была посвящена исследованию ионофореза. В коллоидных системах, как и вообще в растворах, нет электрического тока как такового – носителями зарядов и тока всегда выступают ионы. Поэтому электрический ток и диффузионные потоки можно рассматривать как комбинации потоков отдельных ионов. Выражение для производства энтропии было преобразовано в виде суммы вкладов от потоков отдельных ионов, вызванных перепадами соответствующих электрохимических потенциалов. Появилась милая сердцу каждого теоретика симметрия всех термодинамических сил и потоков, которая кардинально упрощала рассмотрение многокомпонентных растворов (содержащих ионы более чем двух сортов; перед этим все теоретические модели ограничивались случаем одного сорта катионов и одного сорта анионов). В чистом виде ионофорез коллоидов (т.е. движение коллоидных частиц в поле градиента электрохимического потенциала только одного сорта ионов) вряд ли мог наблюдаться в эксперименте, но как теоретический подход для рассмотрения целых серий кинетических явлений он не имеет конкурентов.
В последние годы существования СССР у нас завязались довольно оживленные научные контакты с Вычислительным центром Научного центра биологических исследований (Пущино на Оке под Москвой). Коллеги из этого центра имели совсем другую подготовку – они были математиками, для которых качественная теория дифференциальных уравнений была самой простой вещью (а я только издали присматривался к этой премудрости). Они занимались моделированием процессов переноса в биологических структурах, и наши результаты по ионофорезу оказались для них интересным, поскольку в биосистемах наличие нескольких сортов ионов – правило, а не исключение. Результатом сотрудничества были совместные с Геннадием Денисовым статьи по ионофорезу и дифузиофорезу.
Моделирование неоднородности
Каждая коллоидная система – это воплощенная неоднородность, она неоднородна уже в силу наличия дисперсной фазы. Но в таких системах существуют другие уровни неоднородностью – как крупные, так и мельче коллоидной частицы. Неоднородности мельче коллоидной частицы связаны с дискретностью зарядов. Электрический заряд частицы состоит из элементарных зарядов центров ионизации на ее поверхности. Когда этих центров много, они расположены близко и их дискретностью можно пренебречь, считая заряд распределенным равномерно по всей поверхности (на этом предположении строились все теоретические модели). Когда же центров мало, поверхность можно рассматривать как мозаику, образованную из элементарных зарядов и незаряженных участков. Попытки математического моделирования этого явления привели меня к понятию мозаичного пограничного слоя, в рамках которого чувствуется влияние мозаичности. Мозаичность проявлялась, когда толщина этого слоя превышала толщину двойного слоя.
Более крупные неоднородности я моделировал как вариации объемной доли частиц и исследовал влияние этого явления на электропроводность системы.
Еще один аспект такой неоднородности был связан с электродами – непременными участниками процесса измерения. В переменном электрическом поле, которое обычно используется во время измерений электропроводности, коллоидные частицы испытывают электрофоретические колебания. Те частицы, которые находятся вблизи электродов, при этих колебаниях меняют долю поляризационных зарядов, которые выделяются на электроде, что проявляется как дополнительный ток. Я исследовал этот удивительный механизм, который показывает, что даже в таком простом явлении, как протекание электрического тока, глобальная неоднородность системы в виде электродов имеет определенное значение.
Колебания адсорбции и низкочастотная дисперсия
Чрезвычайно интересный новый аспект был исследован мной в явлении низкочастотной диэлектрической дисперсии коллоидных растворов. Это явление было открыто экспериментально довольно давно. Оно заключалось в том, что водная дисперсия коллоидных частиц в низкочастотном эклектичное поле показывала чрезвычайно высокую емкость (диэлектрическую проницаемость), как будто сегнетоэлектрик. Базовая теоретическая модель этого яркого эффекта была построена Духиным и Шиловым. Причиной необычной емкости была концентрационная поляризация тонкого двойного слоя частиц.
Эта теория достаточно хорошо согласовывалась с экспериментом и была всеми признана в качестве причины явления. Но более детальное рассмотрение показывало, что теория предполагала определенный максимум проницаемости, который не зависел от параметров системы; в то же время экспериментально наблюдались значения проницаемости, превышавшее этот порог, и было неясно, какие еще дополнительные процессы вносят вклад в это явление.
Теоретическое рассмотрение было ограничено моделью бинарного электролита (один сорт катионов и один сорт анионов). Введение большего количества сортов ионов только осложняло высчисления и, казалось, не вносило ничего нового в общую картину. Изменения концентраций ионов, которые были первопричиной дисперсии, были ограничены требованием локальной электронейтральности участков двойного слоя.
Я заметил, что в системе с двумя сортами противоионов требование локальной электронейтральности не так сильно ограничивает перепады концентраций, так как увеличение концентрации одного противоиони могло компенсироваться уменьшением концентрации другого при соблюдении баланса электронейтральности. Эта идея оказалась весьма перспективной и вызвала целый ряд статей. Основную массу вычислений провели я и Илья Разилов. Наши вычисления показали, что эти колебания адсорбции действительно могут повысить диэлектрическую проницаемость системы выше порога для бинарных систем.
Таковы были основные результаты моих исследований в коллоидной науке.

